Learning Strategies and Training

A closer look at imitation learning and self-play reinforcement in SPAG

In this section, we cover:

• Adapting LLMs to game rules via imitation learning
• Transitioning from GPT-4 demonstrations to self-play
• Offline RL approaches and reward shaping
• Balancing specialized training with broader language abilities

3. Learning Strategies & Training

Having established the adversarial game in Section 2, the paper now describes how the LLM is trained to act as both Attacker and Defender, and how it ultimately refines its reasoning capabilities. The overall process occurs in two main stages:

1. Imitation Learning – where the LLM learns from GPT-4’s demonstrations of the game, ensuring it follows the rules and develops basic proficiency in both roles.
2. Self-Play Reinforcement Learning – where the model competes against itself (a copy of its own policy), generating game episodes offline and updating its parameters to maximize (or minimize) the adversarial reward.

Beyond these broad stages, the authors detail policy optimization methods, offline RL considerations, and additional stability techniques that prevent the model from catastrophically forgetting general language capabilities. This section provides a comprehensive explanation of each component.

3.1 Imitation Learning with GPT-4

Motivations for an Initial Imitation Phase

While LLMs are highly capable language generators, they do not a priori know the specific rules of Adversarial Taboo nor how to conform to them. If the model is simply thrown into self-play from scratch, it might violate the game instructions (e.g., the Attacker might explicitly reveal the target word, or the Defender might guess without any evidence). Therefore, the paper introduces an imitation learning (IL) phase:

• Game Awareness: Ensure the model comprehends the concepts of “attacker,” “defender,” “target word,” and “prohibited utterances.”
• Basic Strategy & Etiquette: Demonstrate typical turn-taking, rule-following behavior, and fundamental examples of cunning hints or safe guesses.
• Leverage GPT-4 Quality: GPT-4 has robust reasoning and rule-following abilities. Recording GPT-4’s self-play dialogues yields high-quality trajectories for IL.

Data Collection & Setup

The authors enlist GPT-4 to play the Taboo game against itself, using system prompts that specify who is the Attacker and who is the Defender. For each target word $w$, GPT-4 generates a full multi-turn episode. This yields a dataset $\mathcal{T}_{\text{im}}$ of (state, action) pairs:

1. Attacker Episodes: If GPT-4’s Attacker eventually wins, that game’s action sequences are assigned to an “attacker-winning” subset, $\mathcal{T}_{\text{im}}^{\text{attack}}$.
2. Defender Episodes: Conversely, if the GPT-4 Defender wins, the sequences go into $\mathcal{T}_{\text{im}}^{\text{defend}}$.
3. Ties or Invalid Rounds: Typically discarded or handled separately, as they provide less straightforward examples of “winning moves.”

Because GPT-4 is a powerful model, the authors trust that these demonstrations illustrate reasonable strategies without systematically exploiting obvious shortcuts or ignoring instructions.

Imitation Loss

For the LLM parameterized by $\theta$, the IL objective is to match the probability distribution of winning demonstrations from GPT-4. Let $\pi_{\text{ref}}$ be the base pretrained model (e.g., LLaMA-2, Baichuan-2) before any fine-tuning. Then, for the attacker-winning trajectories, the paper defines:

$$L_{\text{im}}^{\text{attack}}(\pi_\theta) \;=\; - \mathbb{E}_{\tau \in \mathcal{T}_{\text{im}}^{\text{attack}}} \Bigg[ \frac{1}{T} \sum_{t=1}^{T} \log \pi_\theta\!\bigl(u_t \,\big|\, f_{\text{attack}}\!(s_{t-1})\bigr) \;+\; \beta_1 \,\text{KL}\bigl[\pi_\theta \,\big\|\, \pi_{\text{ref}}\bigr] \Bigg],$$

where $u_t$ is the attacker’s chosen utterance at turn $t$, $s_{t-1}$ is the prior state, and $f_{\text{attack}}(\cdot)$ is the prompt template that instructs the model to respond as Attacker. The first term enforces maximum likelihood matching of GPT-4’s moves, while the second term is a KL regularizer with coefficient $\beta_1 > 0$, discouraging the model from drifting too far from its pretrained linguistic knowledge.

Similarly, for defender-winning trajectories:

$$L_{\text{im}}^{\text{defend}}(\pi_\theta) \;=\; - \mathbb{E}_{\tau \in \mathcal{T}_{\text{im}}^{\text{defend}}} \Bigg[ \frac{1}{T} \sum_{t=1}^{T} \log \pi_\theta\!\bigl(v_t \,\big|\, f_{\text{defend}}\!(s'_t)\bigr) \;+\; \beta_1 \,\text{KL}\bigl[\pi_\theta \,\big\|\, \pi_{\text{ref}}\bigr] \Bigg].$$

The total IL loss is typically an average:

$$L_{\text{im}}(\pi_\theta) \;=\;\frac{1}{2}\, L_{\text{im}}^{\text{attack}}(\pi_\theta) \;+\;\frac{1}{2}\, L_{\text{im}}^{\text{defend}}(\pi_\theta).$$

In practice, the model is trained on attacker-winning and defender-winning episodes separately, ensuring it sees both perspectives and inherits GPT-4’s well-structured gameplay.

Outcome of Imitation Learning

By the end of this phase, the LLM can:

• Act in compliance with the Taboo rules (e.g., an Attacker that never blurts out the target word, a Defender that guesses exactly once).
• Demonstrate baseline success in the game, albeit limited by the demonstration data.

It is not yet fully optimized—GPT-4’s moves are strong but not necessarily exhaustive of all strategies. This is why the paper proceeds to a self-play regime next.

3.2 Transitioning to Self-Play

Motivation for Self-Play

Post-imitation, the model has learned “good enough” gameplay but might still exhibit suboptimal or predictable moves. Human data or GPT-4 data alone can be expensive to scale. Self-play offers a powerful alternative: the model generates new episodes on its own, effectively creating an unlimited supply of training data as it iteratively improves.

Moreover, the adversarial nature of Taboo means any deficiency in the Attacker’s cunning or the Defender’s inference will be exploited by the other role. This mutual feedback loop is what drives more sophisticated behavior—analogous to how, in board games, a strategy that once sufficed is later recognized and countered by an improving opponent.

Practical Mechanism

The paper details how a copy of the model, $\pi_{\theta'}$, is made at each iteration. One copy is assigned the Attacker role, another copy the Defender role. A large set of target words $\{w_i\}$ is sampled. For each $w_i$, the Attacker–Defender pair engages in a multi-turn game until it reaches a conclusion: attacker win, defender win, or tie.

This generates a dataset of self-play trajectories, denoted $\mathcal{T}_{\theta'}$. The next step is to apply reinforcement learning updates to $\pi_\theta$ using $\mathcal{T}_{\theta'}$. Crucially, the entire process can iterate multiple times, producing increasingly difficult or clever dialogues.

3.3 Reinforcement Learning from Self-Play

Zero-Sum Objective

Recall from Section 2.3 that we have a zero-sum reward structure:

• If the Attacker succeeds in tricking the Defender, $R(\tau) = +1$.
• If the Defender correctly identifies the target word, $R(\tau) = -1$.
• Ties typically yield $R(\tau) = 0$.

For a trajectory $\tau$, let $\mu_\theta$ denote the Attacker policy and $\nu_\theta$ the Defender policy, both instantiated by the same LLM with different prompts. The training goal is to maximize the Attacker’s expected return if we are focusing on $\mu_\theta$, and minimize that same return if we are focusing on $\nu_\theta$. Symbolically,

$$\max_{\mu} \min_{\nu} \; \mathbb{E}_{\tau \sim (\mu\times\nu)} \bigl[R(\tau)\bigr].$$

When using a single model $\pi_\theta$ for both policies, the authors effectively do separate RL updates for the Attacker component and the Defender component on their respective winning trajectories.

Offline RL and the Importance of Stability

A naive approach might attempt online RL, sampling a trajectory, updating the model, then sampling more episodes from the updated policy. However, online RL is computationally expensive for LLMs, since each iteration requires tens of thousands of dialogues. Hence, offline RL is used: a batch of self-play episodes is collected once from $\pi_{\theta'}$; then $\pi_\theta$ is improved offline on that fixed batch.

Key Stability Concern: LLMs are prone to catastrophic forgetting or degenerate optimization if large policy updates are made from static data. The authors incorporate:

1. KL Regularization w.r.t. $\pi_{\theta'}$ to constrain the updated policy from straying too far in a single step.
2. SFT Data Mixing to preserve general language capabilities, blending in supervised instruction data with the RL objectives.

3.4 Policy Optimization and Loss Functions

Advantage-Based Offline Updates

Let $\mathcal{T}_{\theta'}$ be the self-play dataset collected from the “frozen” policy $\pi_{\theta'}$. For each trajectory $\tau$, define an advantage function $A^{\pi_{\theta'}}(s, a)$ that measures the relative value of action $a$ in state $s$ compared to a baseline. In practice, the authors approximate:

$$A^{\pi_{\theta'}}(s, a) \;\approx\; r(s, a) \,+\, \gamma \, V^{\pi_{\theta'}}\bigl( s' \bigr) \;-\; V^{\pi_{\theta'}}(s),$$

where $\gamma$ is a discount factor, $r(s,a)$ is the immediate reward, and $V^{\pi_{\theta'}}$ is the value function. They then use importance sampling to update $\pi_\theta$:

$$\Delta \theta \;\;\propto\;\; \mathbb{E}_{\tau \in \mathcal{T}_{\theta'}} \Biggl[ \sum_{t=1}^T \frac{\pi_\theta(a_t \mid s_{t-1})}{\pi_{\theta'}(a_t \mid s_{t-1})} \;A^{\pi_{\theta'}}(s_{t-1}, a_t) \;\nabla_\theta \log\,\pi_\theta(a_t \mid s_{t-1}) \Biggr].$$

ReST (Reinforced Self-Training) Approach

A notable simplification is the adoption of a threshold-based approach akin to ReST, where only the winning episodes for each role are used for that role’s policy update. Specifically:

• For the Attacker, filter episodes where $R(\tau) > 0$.
• For the Defender, filter episodes where $R(\tau) < 0$.

Such “self-imitation” techniques (also explored in prior RL literature) help the policy reinforce only successful trajectories, stabilizing training. Episodes with negative returns for a given role effectively do not feed into the gradient for that role.

KL Regularization & Multi-Objective Loss

To prevent the updated policy from diverging from $\pi_{\theta'}$ or forgetting crucial language skills, the final self-play training objective is typically expressed as:

$$L_{\text{SPAG}}(\pi_\theta) \;=\; -\frac12\, \mathbb{E}_{\tau \in \mathcal{T}_{\theta'}^{\text{attack-win}}} \Bigl[ \sum_{t} \frac{\pi_\theta(u_t\mid f_{\text{attack}}(s_{t-1}))} {\pi_{\theta'}(u_t\mid f_{\text{attack}}(s_{t-1}))} \;A^{\mu_{\theta'}}(s_{t-1}, u_t) \;-\; \beta_2 \,\text{KL}\bigl[\pi_\theta \|\pi_{\theta'}\bigr] \Bigr]$$

$$-\frac12\, \mathbb{E}_{\tau \in \mathcal{T}_{\theta'}^{\text{defend-win}}} \Bigl[ \sum_{t} \frac{\pi_\theta(v_t\mid f_{\text{defend}}(s'_{t}))} {\pi_{\theta'}(v_t\mid f_{\text{defend}}(s'_{t}))} \;A^{\nu_{\theta'}}(s'_{t}, v_t) \;-\; \beta_2 \,\text{KL}\bigl[\pi_\theta \|\pi_{\theta'}\bigr] \Bigr] \;-\; \alpha\, \mathbb{E}_{(x,y)\sim D_{\text{SFT}}} \bigl[\log\,\pi_\theta(y\mid x)\bigr].$$

Here:

• $\beta_2$ is a KL coefficient controlling the update magnitude.
• $\alpha$ scales the supervised fine-tuning (SFT) term to maintain general linguistic competence.

The authors note that this mixture of RL on winning episodes plus supervised data offers the best of both worlds: it capitalizes on emergent strategies from self-play while anchoring the model to broader language skills.

3.5 Offline RL and Episode Collection

Sampling Process (Algorithmic View)

The paper provides Algorithm 1 (for data collection) and Algorithm 2 (for iterative self-play epochs). In essence:

1. Copy Model: Create $\pi_{\theta'}$ as a snapshot of the current policy.
2. Generate Episodes:

• For each $w \in V_{\text{target}}$, have $\pi_{\theta'}$ self-play one Taboo match as Attacker vs. Defender.
• Log all states, actions, and final outcomes (win/loss/tie).
  3. Filter & Update: Split episodes into attacker-winning $\mathcal{T}_{\theta'}^{\text{attack-win}}$ and defender-winning $\mathcal{T}_{\theta'}^{\text{defend-win}}$. Apply the RL objective in an offline manner.
  4. Repeat: Once training converges or a set number of epochs is reached, move on to final evaluation.

Convergence & Practical Considerations

• Epochs of Self-Play: The paper typically runs multiple epochs (e.g., 1 to 3) of self-play. Each epoch yields a new policy that is more skilled than the previous.
• Computational Cost: Although massive, the offline nature reduces the overhead compared to naive online RL, since one large batch of dialogues can be generated, then used for multiple gradient passes.
• Incentive to Communicate Less: Because each side can lose by “revealing too much,” the authors observe that over time the conversations tend to become more succinct or strategic, a phenomenon evidenced in the reported game-play dynamics.

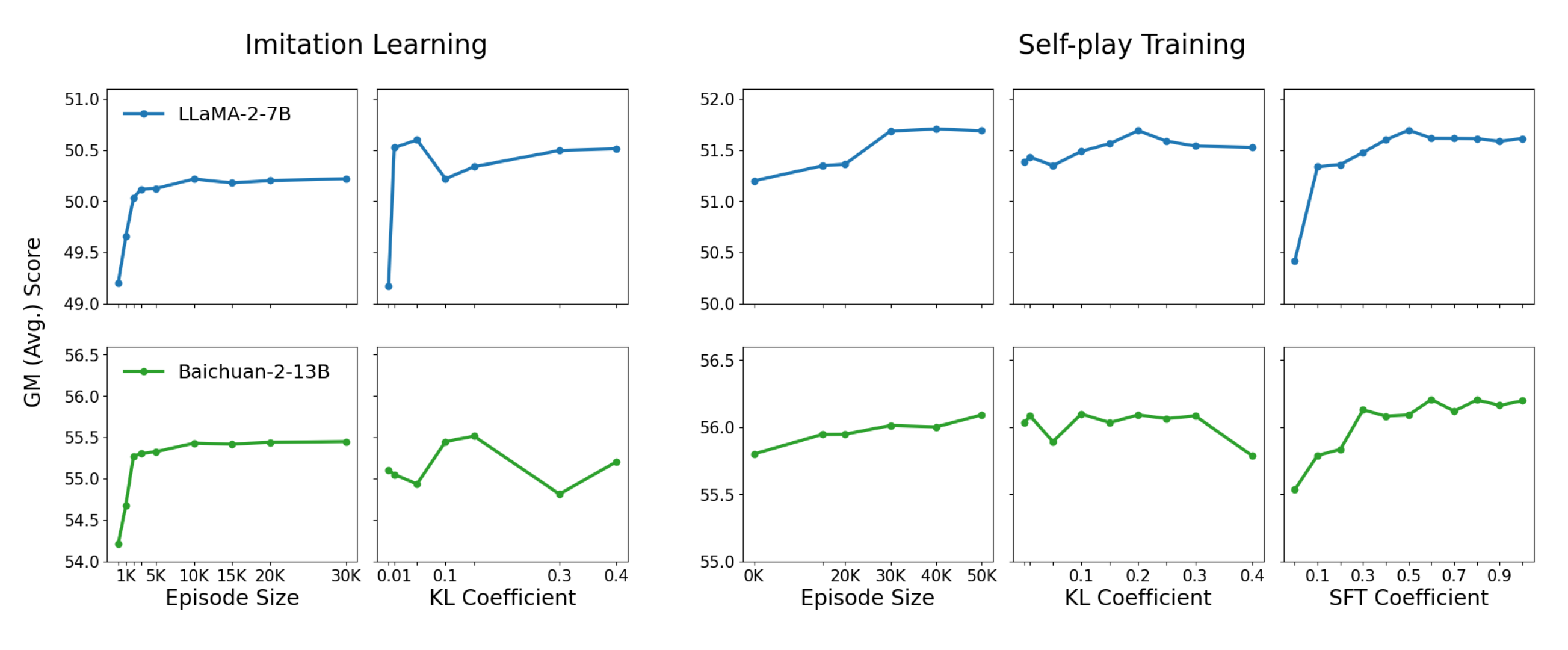
Figure 3, showing ablation studies on hyperparameters such as episode size, KL coefficients, and SFT mixing ratios, indicating sample efficiency and performance trends in reasoning tasks. This figure validates the effectiveness of the offline RL approach.

Summary of Section 3

1. Imitation Learning: GPT-4 data is used to warm-start the LLM, ensuring adherence to game rules and basic strategic proficiency.
2. Transition to Self-Play: The model then generates its own adversarial dialogues, greatly expanding the variety of training examples.
3. Reinforcement Learning: A zero-sum reward structure, offline dataset of self-play episodes, and advantage-based policy updates converge to more refined gameplay.
4. Stability Mechanisms: KL regularization and a persistent SFT term safeguard against overfitting on the game at the expense of overall language quality.

Section 4 will turn to experimental results, showing how these learning strategies boost both in-game performance (win rates, compliance with Taboo rules) and general reasoning as measured on external NLP benchmarks.