Hardware-Aligned and Training Optimizations

Exploring hardware-focused strategies and end-to-end training techniques for NSA

In this section, we cover:

• Hardware-aligned optimizations and kernel design
• Efficient backpropagation in sparse architectures
• Techniques for end-to-end trainability in NSA

Welcome to Part 4 of this series on the NSA paper, which details how the proposed Native Sparse Attention (NSA) is engineered for efficiency on modern hardware and how it remains fully trainable end-to-end. This section covers two major themes: optimizing the attention mechanism for hardware (ensuring high runtime efficiency on GPUs) and designing the method to be trainable from scratch (addressing gradient flow and backpropagation). We examine each sub-part in detail below.

4.1 Hardware-Aligned Optimizations

NSA introduces hardware-aligned innovations to transform theoretical sparsity gains into actual speedups on modern accelerators. A key principle in NSA’s design is balancing arithmetic intensity – the ratio of compute operations to memory accesses – to match GPU capabilities (⇒) (⇒). Modern GPUs like the NVIDIA A100 have immense compute throughput (e.g. via Tensor Cores) but can be bottlenecked by memory bandwidth if an algorithm performs too little computation per data fetched (⇒). NSA’s algorithm is therefore crafted to increase compute utilization and reduce memory stalls, achieving a balance where the GPU stays in a compute-bound regime during training (full-sequence attention) and minimizes memory access during decoding (generating one token at a time) (⇒). By identifying that training/prefill phases and autoregressive decoding have different bottlenecks, NSA sets different optimization goals for each: reduce computation cost in training/prefilling, and reduce memory access in decoding (⇒) (⇒). This insight guides several of NSA’s hardware-aligned strategies.

Blockwise memory access is at the heart of NSA’s hardware optimizations. Instead of attending to arbitrary scattered tokens, NSA selects and processes tokens in contiguous blocks in memory. This design is motivated by GPU hardware characteristics: GPUs achieve much higher throughput for coalesced (continuous) memory accesses compared to random accesses (⇒). By dividing the sequence into fixed-size blocks and choosing entire blocks of tokens for attention, NSA ensures that when data is loaded from GPU global memory (HBM), it comes in large contiguous chunks, fully utilizing memory bandwidth. Moreover, operating on block matrices aligns well with GPU Tensor Cores, which are optimized for matrix multiply operations on block tiles (⇒). In fact, blockwise processing has become a fundamental principle in high-performance attention implementations (FlashAttention also uses block tiling) (⇒). NSA explicitly adopts this principle: “Blockwise selection is crucial to achieve efficient computation on modern GPUs” (⇒). It exploits the observed spatial continuity of attention scores – nearby tokens often have similar importance (⇒) – by always selecting a group of neighboring tokens rather than single token indices. This not only preserves attention to important regions but also caters to hardware by reading memory in bulk.

Another hardware-aligned innovation is NSA’s memory access pattern and caching strategy for key-value (KV) data. In models with Grouped-Query Attention (GQA) or similar, multiple heads share the same KV cache, meaning they would fetch the same keys/values during attention (⇒). NSA takes advantage of this by ensuring that all heads in a group select the same blocks of keys/values (KV) for attention. In other words, the sparse attention pattern is made consistent across heads within a group (⇒) (⇒). This yields two benefits: (1) It avoids redundant memory loads – a particular block of keys is fetched once and used for all heads in the group, instead of each head loading it separately. (2) It simplifies the memory layout, as the union of selected tokens for the group is just those few blocks, improving cache locality. This idea is reflected in Equation (10) of the paper, where the importance scores of blocks are aggregated across all heads in a group, ensuring a unified selection (⇒) (⇒). By aligning the selection across heads, NSA minimizes KV cache misses and maximizes reuse, which is crucial in the decoding phase when keys/values reside in a cache. The authors note that without such grouping, methods that let each head choose tokens independently fail to reduce memory access in GQA models, since the union of all heads’ selections can be large (⇒). NSA avoids this pitfall by design.

Overall, these hardware-aligned optimizations lead to significant efficiency improvements. NSA’s attention has a much smaller working set per query token than full attention, which means far fewer memory transactions and higher effective utilization of the GPU. In the training/prefill stage (processing long sequences in one go), NSA’s hierarchical strategy (compression + selection + local window) reduces computation such that the GPU’s compute units are well-utilized (no time wasted waiting on memory) (⇒) (⇒). In the decoding stage (generating tokens one by one with a cache), NSA drastically limits how much of the cache must be read for each new token. For example, at a 64k sequence length, NSA only needs to load on the order of a few thousand tokens worth of key/value data (from compressed, selected, and local windows) for each attention operation, compared to tens of thousands in full attention (⇒) (⇒). Table 4 of the paper shows that at 64k context, NSA accesses only ~5.6k “tokens” of memory vs. 65k for full attention, an ~11.6× reduction, which translates to an ~11.6× speedup in a memory-bound scenario (⇒) (⇒). Similarly, during full-sequence forward/backward passes, NSA’s sparse computation and data reuse yield progressively larger speedups as sequence length grows (since full attention cost grows quadratically while NSA grows much slower) (⇒). These improvements are hardware-realized: experiments confirm NSA achieves substantial wall-clock speedups (not just theoretical) across decoding, forward, and backward phases on an 8×A100 GPU system (⇒). In summary, NSA’s attention mechanism is carefully aligned with hardware: contiguous block processing, coalesced memory reads, and shared cache usage all contribute to maximizing throughput on modern accelerators (⇒) while preserving the essential information for the model.

4.2 Kernel Design on Modern Accelerators

To unlock the above benefits, NSA relies on a custom kernel design tailored for modern GPU architectures. The implementation is built using Triton, a specialized GPU programming framework that allows writing efficient kernels at a high level (⇒). NSA’s authors integrate their sparse attention with Triton-based operations, leveraging existing high-performance kernels where possible and introducing new ones for the novel components. Notably, the compression and sliding window branches of NSA’s attention can be executed with minimal changes to existing FlashAttention v2 kernels (since these branches still operate on contiguous segments similar to standard attention) (⇒). The real challenge is the sparse selection branch, where each query may attend to a set of disjoint blocks of keys – a pattern not handled by off-the-shelf kernels. For this, the authors developed a specialized CUDA/Triton kernel that aligns with NSA’s blockwise sparse pattern (⇒).

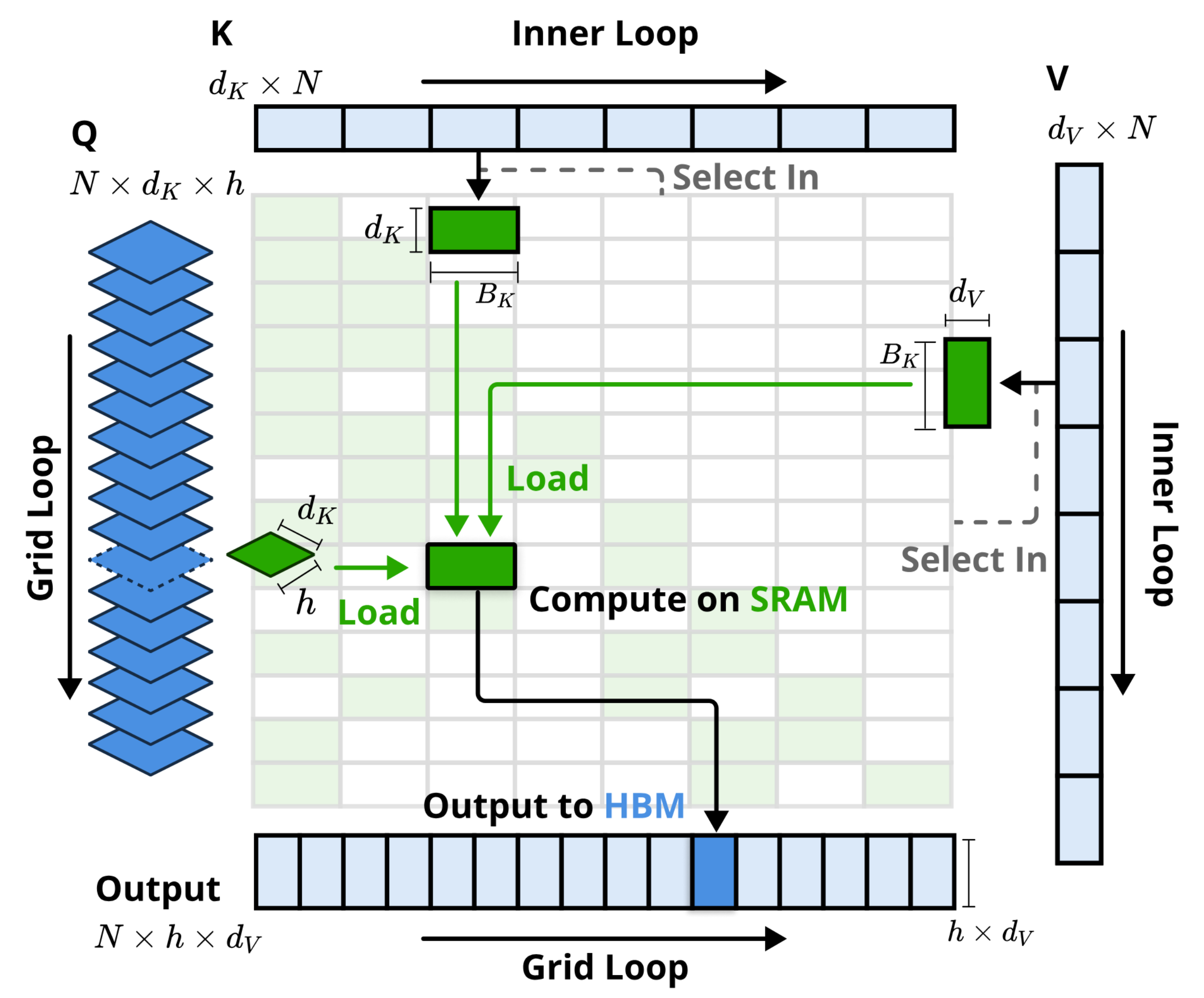
Figure 3 of the paper provides an overview of the NSA kernel’s execution pattern (⇒).

At a high level, the kernel breaks the attention computation into a two-level loop: an outer grid loop over query positions (or blocks of positions), and an inner loop over the selected key/value blocks for each query. The key innovations at the kernel level can be summarized as follows:

1. Group-Centric Data Loading: Instead of processing one attention head at a time or one query block at a time (as in FlashAttention), NSA’s kernel processes queries grouped by GQA sets. For each position $t$ in the sequence (the outer loop), it loads all query vectors for all heads in a GQA group into fast on-chip memory (SRAM/shared memory) together (⇒). These heads share the same selected key/value blocks by design, so this group-wise loading means the subsequent memory fetches of keys/values will be useful to all those heads simultaneously. In practice, this is implemented by taking all queries $Q$ in the group at position $t$ (with shape [heads-per-group, d_k]) and staging them in SRAM, along with the list of that position’s selected block indices $I_t$ for keys/values (⇒). Group-centric loading ensures that we don’t reload queries or repeat work for each head, and it sets up the computation so that one pass over the relevant keys/values serves multiple attention heads.

2. Shared KV Fetching: In the inner loop, the kernel iterates over the list of selected blocks for the current query position. For each such block index in $I_t$, it loads the corresponding block of keys and values from global memory into SRAM (⇒). Crucially, these key/value blocks are stored and fetched as contiguous chunks (each block might be, for example, 64 tokens long, which is a multiple of the block size $l'$) (⇒). By reading continuous blocks, the kernel takes advantage of coalesced memory access – the hardware will fetch an entire cache line or memory segment efficiently. Once a block $B_k$ of keys (of size $B_k \times d_k$) and the matching block of values ($B_k \times d_v$) are in SRAM, the kernel computes the partial attention for all queries in the group on that block (performing the necessary matrix multiplies using the queries already loaded). Then it proceeds to the next block in $I_t$. This sequential block loading strategy minimizes memory overhead: only the needed blocks are transferred, and each transfer brings in a large chunk of data that is fully utilized in computations (⇒). The block size $B_k$ is chosen to be a divisor of the selection block length $l'$, aligning with the blockwise scheme (⇒). This also makes the data well-suited for Tensor Core operations (which prefer standard tile sizes), maximizing hardware multiply-accumulate throughput (⇒).

3. Grid-Based Outer Loop Scheduling: The outer loop iterates over query positions (or blocks of positions) and is implemented using Triton’s grid mapping of threads/blocks to data (⇒). Since each query position $t$ in NSA attends to roughly the same number of total tokens (the selected $n$ blocks + compressed + local window, which is fixed or near-constant for all $t$), the workload per query is balanced. NSA leverages this by distributing different query positions across the GPU’s streaming multiprocessors in a balanced way – each GPU thread block handles one (or a small set of) query positions, and each does a similar amount of work (⇒). This grid scheduling ensures there are no load imbalances (no one warp is stuck doing significantly more work than another), which helps achieve maximum parallelism. By pulling the outer loop into the GPU’s grid, the kernel avoids launching separate operations for each position; instead, many queries are computed in parallel within one unified kernel launch. This makes the entire attention computation a single fused kernel, reducing launch overhead and allowing the compiler to optimize across the loops.

These kernel-level optimizations enable NSA to reach near-optimal hardware utilization. As the authors note, the design “eliminates redundant KV transfers through group-wise sharing and balances compute workloads across GPU SMs”, achieving near-optimal arithmetic intensity (⇒). In other words, the GPU spends most of its time doing math on loaded data rather than waiting on memory. The use of on-chip SRAM (shared memory) to hold queries and blocks means that once data is loaded, all subsequent operations are done at SRAM speed (much faster than global memory). Figure 3 in the paper illustrates this process, with green blocks denoting data in SRAM and blue blocks for data in HBM (global memory) (⇒). The queries are loaded (green $Q$ block), then each selected key/value block is brought in (blue to green $K, V$ blocks) for computation, and finally the output is written back to global memory (blue output) (⇒). By carefully orchestrating data movement in this way, NSA’s custom kernel is able to execute the sparse attention extremely efficiently on GPUs, rivaling the performance of dense attention kernels (FlashAttention) despite the irregular access pattern. Importantly, the authors implemented both forward and backward passes of this kernel in Triton (or CUDA) to fully support training (⇒) – we will discuss the backpropagation aspect in Section 4.4. In summary, NSA’s kernel design uses custom GPU kernels (via Triton) that exploit grouped data loading, contiguous memory fetches, and parallel loop scheduling to fully leverage modern accelerator features (like Tensor Cores and wide memory buses), thereby delivering the large speedups promised by the sparse algorithm (⇒) (⇒).

4.3 Enabling End-to-End Trainability

A central contribution of NSA is that it is natively trainable – the sparse attention mechanism is integrated into the model from the start and supports end-to-end training (backpropagation) without any proxies or retraining of a dense model (⇒). This is in contrast to many prior sparse attention methods that apply sparsity only at inference or use a pretrained dense model, which can lead to suboptimal performance and difficulties in learning sparse patterns (⇒). NSA’s authors identified two major issues with earlier approaches: first, applying sparsity only after pretraining tends to degrade performance (the model wasn’t optimized for it), and second, many sparse methods include non-differentiable steps (like clustering, hard top-$k$ sampling, or hashing) that break gradient flow (⇒) (⇒). Such components create “discontinuities in the computational graph” and prevent the model from learning the attention pattern during training (⇒). NSA explicitly avoids these pitfalls by designing the entire sparse attention pipeline to be differentiable (or at least gradient-inclusive) and by training the model from scratch with the sparse attention active. This training-aware design is highlighted as NSA’s second core innovation: “Enable stable end-to-end training through efficient algorithms and backward operators” (⇒). Below, we detail how NSA achieves full trainability with minimal overhead and stable learning dynamics.

Hierarchical attention with gating: NSA’s attention mechanism is composed of three differentiable branches – compression, selection, and sliding window – which are combined with a learned gating mechanism. As illustrated in Figure 2, the input sequence for each attention layer is processed by three parallel mappings: (1) a coarse-grained compressed attention that summarizes the whole sequence into a smaller set of representative tokens, (2) a fine-grained selected attention that picks out the most important tokens or blocks for each query, and (3) a sliding window local attention that focuses on a recent context window for fine local details (⇒). The outputs of these branches are then blended together for each query position. Formally, NSA defines the attention output for query token $t$ as a weighted sum of the three branch outputs:

$$o^*_t \;=\; g^{(\text{cmp})}_t \cdot \text{Attn}(q_t, \widetilde{K}^{(\text{cmp})}_t, \widetilde{V}^{(\text{cmp})}_t)\;+\;g^{(\text{slc})}_t \cdot \text{Attn}(q_t, \widetilde{K}^{(\text{slc})}_t, \widetilde{V}^{(\text{slc})}_t)\;+\;g^{(\text{win})}_t \cdot \text{Attn}(q_t, \widetilde{K}^{(\text{win})}_t, \widetilde{V}^{(\text{win})}_t)$$

where $\widetilde{K}^{(cmp)}_t, \widetilde{V}^{(cmp)}_t$ are the compressed keys/values, $\widetilde{K}^{(slc)}_t, \widetilde{V}^{(slc)}_t$ the selected keys/values, and $\widetilde{K}^{(win)}_t, \widetilde{V}^{(win)}_t$ the sliding window keys/values for the query at position $t$. The coefficients $g^{(cmp)}_t$, $g^{(slc)}_t$, $g^{(win)}_t$ are gate values in [0,1] that sum (approximately) to 1, determining the contribution of each branch (⇒) (⇒). Importantly, these gate values are not fixed; they are produced by a small neural network (an MLP with sigmoid activation) based on the query’s features (⇒). This means the gating is learned and dynamic – during training, the model can adjust how much it relies on each branch for each token. Because the gates are generated via a differentiable function (MLP + sigmoid), they allow gradient propagation: the model can smoothly shift attention emphasis among the three components as needed, and the gating network’s parameters are trained by gradient descent like any other part of the model.

All components of NSA’s attention are designed to be differentiable. The token compression step is implemented by a learnable function $\phi$ that maps a block of raw keys to a single compressed key vector (⇒) (⇒). Specifically, $\phi$ is an MLP that takes the concatenation of keys in a block (with positional encodings) and produces a compressed representation (⇒). This learned compression ensures that the process of condensing tokens is trainable – the model can learn what information to store in the compressed tokens. The token selection step uses attention-based importance scores to decide which blocks to keep. NSA leverages the intermediate scores from the compressed attention branch as a guide: it computes a softmax of the query $q_t$ against the compressed keys $\widetilde{K}^{(cmp)}_t$ to get a probability distribution $p^{cmp}_t$ over compression blocks (⇒) (⇒). These probabilities (which sum to 1) indicate which parts of the sequence are most relevant to the query in a coarse sense. NSA then derives selection-block importance scores from these probabilities. In the simplest case where selection blocks align with compression blocks, the importance of a selection block equals the probability of the corresponding compression block (⇒). If the block sizes differ, a small aggregation (summing probabilities of compression sub-blocks within a selection block) is done (⇒) (⇒). Crucially, this computation is purely based on attention weights and summation – operations that are differentiable. The final act of choosing the top-$n$ blocks based on these scores is a hard selection (discrete), which technically does not have a gradient. However, because the scores themselves come from a softmax (which is differentiable w.r.t. model parameters), the model can still learn to adjust those scores. In practice, this means if a certain token should have been selected but wasn’t, the model can increase its learned importance score (by adjusting $q_t$ or the compressed keys via gradients), so that next time it falls in the top-$n$. This is how gradient signals indirectly influence the selection outcome, even though the argmax operation has no direct derivative. Moreover, no external non-trainable mechanism (like clustering) is used – the selection is an intrinsic part of the attention computation. By keeping the selection criteria tied to attention logits, NSA ensures there are no discontinuities in the training graph due to sparsity. All parameters (queries, keys, the compression MLP, gating MLP, etc.) receive gradients based on the final loss.

NSA also introduces an architectural choice to improve trainability: it provides independent key and value representations for each branch (⇒). This means the keys/values used for the compressed branch, for the selected branch, and for the sliding window are not one and the same (they may originate from the same token, but through separate projection layers). By isolating the representations, NSA prevents interference between the branches during learning (⇒). For example, the model can learn a compressed-key embedding that’s good for coarse summarization, separately from a fine-detail key embedding that’s used when a token is directly attended (selected or in local window). If they shared the exact same key, a gradient that encourages a token to be more important in the compressed view could unintentionally affect its fine-scale behavior. NSA avoids this by effectively splitting the attention heads for different purposes (with minimal overhead in parameters) (⇒). This “prevents shortcut learning across attention branches” and yields stable learning since gradients for long-range context (compression/selection) and local context (sliding window) are handled independently (⇒). Each branch focuses on its pattern (global vs local) without one dominating or trivializing the other. The paper notes that this design introduces only marginal extra cost, but greatly helps “preventing gradient interference between local and long-range pattern recognition” (⇒).

Thanks to these measures, NSA can be trained from scratch on large-scale data without any special tricks or pretraining of a dense model. The authors demonstrate this by pretraining a 27B-parameter Transformer using NSA attention on 260B tokens (⇒). The training process was stable – Figure 4 in the paper shows the pretraining loss curve for NSA versus a Full Attention baseline, and NSA’s loss decreases smoothly and consistently below that of the full-attention model (⇒). There were no spikes or divergences, indicating NSA did not suffer from optimization instabilities. Moreover, NSA actually achieved better final perplexity than the dense baseline, showing that the sparse mechanism did not hinder model capacity (⇒). By the time of fine-tuning and evaluation, the NSA-pretrained model matched or exceeded the quality of a full-attention model on a suite of benchmarks ([2502.11089] Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention). This confirms that NSA’s sparsity is trainable without sacrificing performance – the model can learn effectively with NSA from the beginning. Additionally, NSA’s design preserves long-range information during training, avoiding the issue of the model “forgetting” long context. Because some form of each token’s information is always present (either compressed or, if important, explicitly selected or within the local window), the model can propagate gradients even to far-away tokens when needed. The paper’s conclusion notes that NSA’s hardware-aligned design maintains “sufficient context density to support growing reasoning depth without catastrophic forgetting” (⇒). In other words, even as the model looks at very long sequences, it doesn’t lose the ability to attend to and learn from distant tokens – something that could happen if the sparsity was too aggressive or not properly trained. This, combined with the gating mechanism allowing dynamic adjustment, results in NSA actually improving some long-context abilities relative to dense attention (⇒).

In summary, NSA enables end-to-end trainability by making every component differentiable and learnable, using a gating strategy to blend sparse attention outputs, and structuring the model to avoid gradient conflicts. There are no external clustering steps, no sampled attention that the model can’t influence – the model itself decides what to compress or select through learning. This training-inclusive approach, along with careful architectural choices (like independent branch parameters), ensures that NSA can be optimized with SGD/backpropagation just like a standard Transformer. The result is a sparse attention architecture that learns its sparse patterns during pretraining, thereby retaining full model quality while significantly reducing computation (⇒).

4.4 Efficient Backpropagation in Sparse Architectures

Designing NSA to be trainable is one aspect; implementing the backpropagation efficiently is another crucial aspect, given the complexity of the attention mechanism. Sparse operations can sometimes introduce overhead in the backward pass (for example, handling gradients for a variable selection of tokens, or inefficiently using hardware if not carefully optimized). NSA addresses this by providing optimized backward operators as part of its hardware-aligned design (⇒). In practice, the authors wrote custom backward-pass logic (likely also in Triton/CUDA) for their sparse attention kernel, ensuring that gradient computation is as efficient and scalable as the forward pass. The result is that NSA enjoys speedups in training throughput (which includes backward) comparable to its inference speedups. Empirical measurements showed that for long sequence lengths, NSA’s training step (forward + backward) is much faster than full attention. Specifically, at 64k sequence length, NSA achieved up to a 6× speedup in the backward pass (and about 9× in the forward pass) compared to standard attention with FlashAttention, when measured on the same hardware (⇒). This indicates that NSA’s backpropagation is not a bottleneck; it scales well with sequence length due to the sparse computations.

One reason backpropagation is efficient is that NSA’s sparsity reduces the amount of work and memory in the backward pass just as it does in the forward pass. In a full attention layer, the gradient computation involves $O(L^2)$ operations for sequence length $L$ (similar to forward), and intermediate activations (like the entire attention matrix or softmax probabilities for all $L$ keys per query) might need to be stored or recomputed for gradients. NSA’s mechanism limits each query to interacting with $N_t \ll L$ tokens in total (where $N_t$ is the sum of selected, compressed, and local tokens) (⇒). This means the gradient for each query will only propagate through those $N_t$ token interactions, not $L$. For example, if a query attends to 16 selected blocks (say 16×64 = 1024 tokens), plus a compressed summary of maybe a few hundred tokens, plus a local window of 512, then $N_t$ might be on the order of 2k tokens instead of 64k. Gradients w.r.t. attention scores: In backward pass, one typically needs to compute gradients of the attention weights (from the softmax) and then propagate to queries, keys, and values. NSA’s attention is split across three branches, but thanks to gating, each branch’s output contribution is scaled by $g^{(c)}_t$. The loss gradients flowing back will naturally split into the three branches, weighted by those gates. Since the gates are differentiable, we also get gradients for the gate MLP (which are negligible in cost compared to the attention gradients). Within each branch, the backward computation resembles standard attention but on a much smaller scale (proportional to $N_t$ for that query). For the compressed branch, the backward pass computes gradients for the compressed keys/values and then further backpropagates through the compression MLP $\phi$ to distribute gradients to the original tokens in each block. This is efficient because $\phi$ is applied per block (for instance, a block of 32 tokens compresses to 1, so the backward of $\phi$ redistributes the error to 32 token embeddings, which is trivial compared to attention on thousands of tokens). For the selected branch, backpropagation involves the subset of tokens that were selected. The key difference in NSA’s trainable approach is that those tokens’ original representations do receive gradient (since they were part of the attention computation), whereas in non-trainable setups a token excluded from attention would have no gradient path. NSA’s use of softmax-based importance ensures that if a token was important, it likely was selected and thus got to contribute (hence gets gradient); if it wasn’t selected, any potential effect it could have had is mediated through the compression branch’s gradient. This mechanism avoids wasted computation on unimportant tokens while still providing gradient signals to those that matter for the loss.

From an implementation perspective, NSA’s backward pass is streamlined by reusing the same blockwise strategy as the forward pass. The custom Triton kernel likely computes attention in forward and can be run in reverse: group-wise handling of queries and blocks is equally beneficial for backprop. For instance, the gradient w.r.t. keys in a selected block that was used by a group of heads can be computed once for that block and applied to all heads in the group, rather than separately per head. This mirrors the forward process and avoids redundant work. Similarly, by processing contiguous blocks, the backward kernel can fetch the necessary data efficiently. Modern fused attention kernels (like FlashAttention) typically recompute certain intermediate results on the fly during backward to save memory (for example, redoing the softmax to get the probabilities needed for gradient). NSA can adopt similar tactics: because $N_t$ is small, it’s cheap to recompute the attention softmax over those $N_t$ entries if needed during backward. Thus, NSA can achieve memory-efficient training – it can handle very long sequences without running out of memory, because it never needs to materialize the full $L \times L$ attention map or gradients. The paper specifically notes that NSA supports 64k length sequences with end-to-end training, which would be infeasible with standard attention due to memory constraints, but is made possible by the sparse computation and efficient backprop operators ([2502.11089] Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention).

A noteworthy point is that NSA’s authors compared their training speed against a strong baseline: FlashAttention-2 implemented in Triton (⇒). This means the 6× backward speedup is above and beyond the highly optimized dense attention backward. Achieving this required careful engineering of the backward pass. Although the paper doesn’t delve into low-level code, it emphasizes that both forward and backward kernels are optimized as part of NSA’s design (⇒). By co-designing the algorithm with its implementation, they avoid scenarios where the backward of a sparse method becomes a new bottleneck. For example, if naive, one might implement selection by gathering indices (which could produce scattered memory writes in backward). Instead, NSA’s blockwise approach means the gradient contributions are written in large chunks (coalesced) as well. The loop scheduling in the kernel likely applies to backward similarly, balancing the workload of gradient calculations across threads.

Finally, NSA’s approach to trainability ensures that gradients are used effectively to update the model despite the sparsity. Because the model was trained with NSA from the start, the gradients flowing through the sparse attention are meaningful for the model’s parameters. NSA doesn’t need an extra finetuning stage to adjust to sparsity – the gradients during pretraining already shaped the attention patterns. This end-to-end optimization is evidenced by the model’s strong performance after training. In essence, NSA shows that one can have a highly sparse attention pattern and still backpropagate through it at scale and efficiently. The gradients with respect to all relevant tokens are accounted for, and any token that was ignored by one branch still can get gradient via another branch (compression or local). This holistic gradient coverage means the model can learn where and when sparsity is appropriate. The efficient backward implementation then ensures this learning doesn’t come at a huge computational cost. The outcome is a sparse architecture whose training speed and memory footprint are vastly better than full attention, without giving up the end-to-end learnability. As the authors conclude, NSA “achieves accelerated training and inference while maintaining Full Attention performance” (⇒) – a testament to efficient backpropagation and well-balanced design.

In summary, NSA’s backpropagation is efficient due to the combination of reduced computational complexity (sparse interactions), careful kernel optimization (grouped and coalesced operations in backward as in forward), and maintaining a fully differentiable pipeline (so standard gradient descent applies). The gradients are stored and computed only for the necessary subset of tokens, updated through the same fast paths as forward, and seamlessly integrated into the model update process. This allows training very long-context models with NSA at a fraction of the time and memory cost of dense attention, completing the picture of an attention mechanism that is both fast and trainable end-to-end (⇒) (⇒).