Evaluation, Discussion, and Future Directions

Summarizing the experiments, performance metrics, and broader insights on NSA

In this section, we cover:

• Experimental setup and protocols
• Benchmarking results (speedups, scalability, etc.)
• Visualizations relevant to NSA’s performance
• Limitations, future directions, and concluding remarks

5.1. Experimental Setup and Pretraining Protocol

Model Architecture and Configuration: The NSA model is built on a 27B-parameter Transformer backbone (with ~3B active parameters due to Mixture-of-Experts) following state-of-the-art large language model practices (⇒). It uses Grouped-Query Attention (GQA) (4 query groups, 64 total heads) and a Mixture-of-Experts (MoE) structure (72 experts, top-6 selection) to enhance capacity efficiently (⇒) (⇒). Each attention head has dimension $d_q=d_k=192$ and $d_v=128$, with 30 transformer layers and hidden size 2560 (⇒). This architecture ensures that NSA’s sparse attention mechanism is evaluated in a competitive LLM setting alongside modern techniques like GQA and MoE.

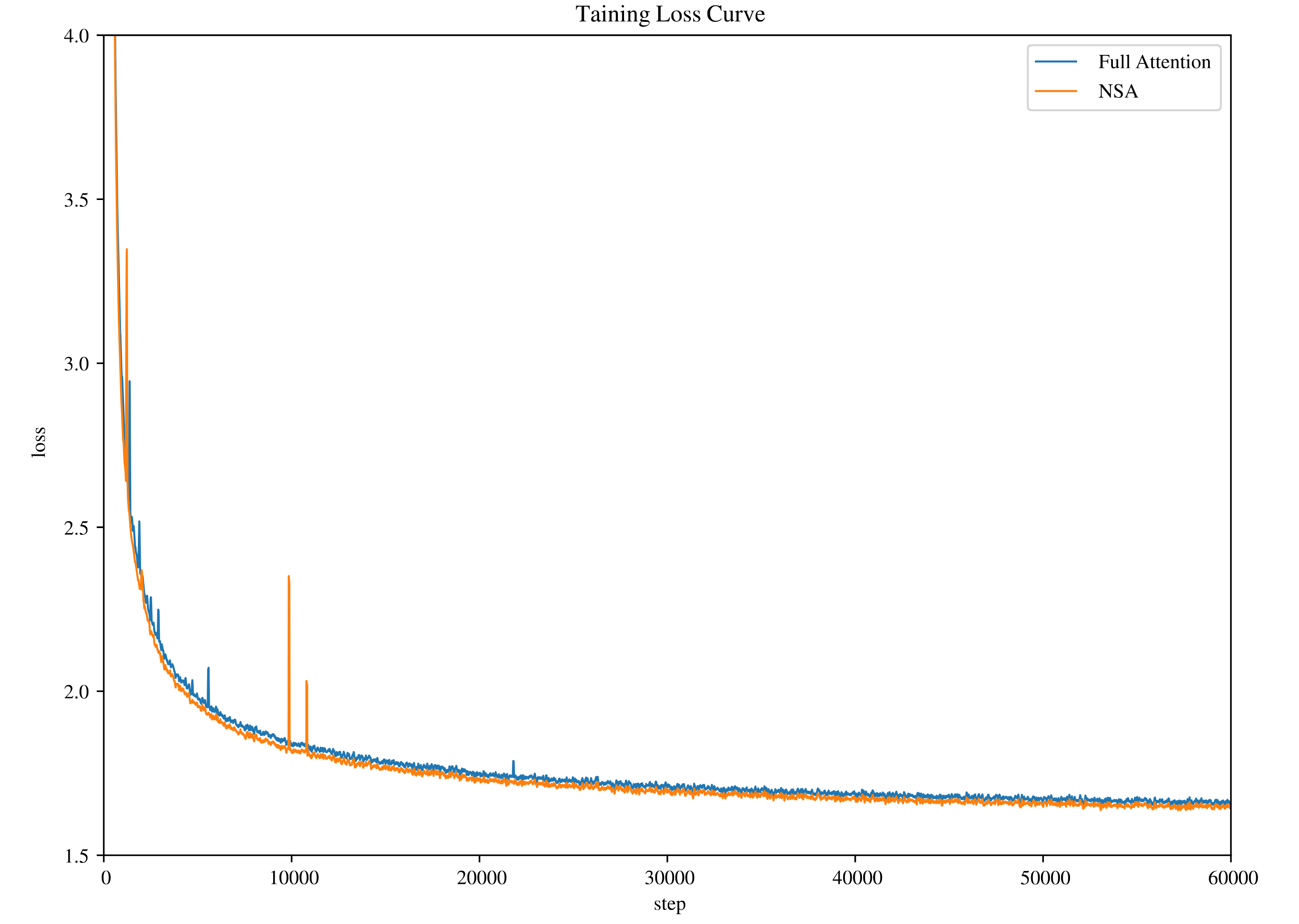
Pretraining and Long-Context Adaptation: Both the NSA model and the full-attention baseline are pretrained from scratch on a large text corpus (about 260–270B tokens) with an 8k token context window (⇒) (⇒). This extensive pretraining regimen is designed to reach full convergence for each model, ensuring a fair performance comparison (⇒). To equip the models with long-context capabilities, the authors continue training (long-context fine-tuning) on 32k-length documents using the YaRN method (a long-context adaptation strategy) (⇒). This two-stage training protocol (pretrain at 8k, then adapt to 32k) allows NSA to learn its sparse attention patterns natively during training. Throughout pretraining, NSA’s training remained stable and convergent – Figure 4 shows that NSA’s loss curve declines smoothly and even reaches a lower final loss than the full-attention model (⇒) (⇒), indicating NSA incurs no optimization instability despite its sparsity. Importantly, both NSA and the dense baseline were trained to full convergence under identical conditions (dataset, number of tokens, etc.), so any performance differences can be attributed to the attention mechanism rather than under-training (⇒).

Evaluation Methodology: The pretrained models are evaluated on a broad array of benchmarks falling into three categories (⇒):

• General Language Benchmarks: Knowledge-intensive and reasoning tasks of typical length (within 8k tokens). The paper reports results on MMLU, MMLU-PRO, CMMLU (knowledge tests), BBH, GSM8K, MATH, DROP (reasoning and math), and MBPP, HumanEval (coding tasks) (⇒) (⇒). These tasks are evaluated in few-shot or zero-shot settings (e.g. 5-shot accuracy for MMLU, etc.) as appropriate, following standard protocols (⇒).

• Long-Context Benchmarks: Tasks specifically designed to test performance with very long inputs (up to 32k–64k tokens). The authors use LongBench (⇒), a suite of long-context tasks including single-document QA, multi-document QA, synthetic long-text tasks, and code completion/retrieval tasks. Examples include needle-in-a-haystack retrieval (64k context), multi-hop QA across long documents (e.g. HPQ, 2Wiki), long report summarization (GovRpt), long conversation understanding, and long code tasks (e.g. LCC) (⇒) (⇒). Performance is measured by accuracy or F1 as appropriate for each subtask, and an overall average score is reported (⇒) (⇒).

• Chain-of-Thought Reasoning: To assess NSA’s ability to handle complex reasoning with long contexts, the authors fine-tune both models on 32k-length mathematical reasoning traces (10B tokens of chain-of-thought data distilled from a stronger model) (⇒). They evaluate on the challenging AIME 2024 math competition problems, comparing an NSA model fine-tuned for reasoning (NSA-R) against an analogously fine-tuned full-attention model (Full Attn-R) (⇒). Each model generates solutions with a 8k or 16k token reasoning budget to see if longer reasoning chains improve accuracy (⇒). This tests NSA’s integration into advanced training paradigms (knowledge distillation for reasoning) and its efficacy on tasks requiring multi-step logical derivations.

Baselines and Comparison Setup: In addition to the full-attention baseline, NSA’s performance is compared against several state-of-the-art inference-only sparse attention methods on the long-context tasks (⇒). These include:

• H2O (⇒): a KV-cache eviction method (dynamically drops least-important tokens from the cache to save memory).

• InfLLM (⇒): a query-aware selection approach that selects key subsets based on query content.

• Quest (⇒): a blockwise selection strategy estimating chunk importance via a heuristic (product of query with key min-max) per block.

• Exact-Top (⇒): an “oracle” baseline that computes full attention scores but then only attends to the top-$n$ scoring keys for each query (mimicking an ideal top-$n$ sparsity).

These baselines cover a range of sparse attention paradigms (cache eviction, learned importance, heuristic selection, etc.) (⇒). For fairness, all sparse methods (including NSA) are configured to have the same overall sparsity level when comparing long-context performance (⇒). Notably, only NSA supports end-to-end training – the other methods cannot be applied during training (they lack trainable operators). Therefore, for general and reasoning evaluations that require training or fine-tuning, the comparison is limited to NSA vs. Full Attention (⇒) (⇒), while the inference baselines are included for long-context tasks.

Ablation Studies – Alternate Sparse Strategies: The authors conducted ablation-like explorations to justify NSA’s design choices by attempting to adapt other sparse attention strategies into a trainable setting. They report significant challenges with these alternatives, which ultimately guided the final NSA architecture:

• Key Clustering Approaches: Methods like ClusterKV group keys/values by similarity into clusters (⇒). In theory these could be trained by attending to a few relevant clusters per query. However, the authors encountered three major issues: (1) high computational overhead from continually clustering tokens on the fly, (2) load imbalance and optimization difficulties (especially with MoE models, where uneven cluster sizes led to straggling experts) (⇒), and (3) complex implementation requirements (needing periodic reclustering and segmented training schedules) (⇒). These factors made clustering-based sparse attention impractical for real-world training, creating bottlenecks that “significantly limit their effectiveness for deployment” (⇒).

• Learnable Block Selection: The authors tried to introduce a differentiable block selection mechanism, where each block’s importance is predicted by a small network and trained with an auxiliary loss (⇒) (⇒). In their test on a 3B-parameter model, this approach required adding extra “representative” key vectors per block and supervising the selection network using true attention scores (⇒). The result was increased operator complexity and a degradation in model performance (higher training loss), suggesting the overhead of the auxiliary mechanism outweighed its benefits (⇒) (⇒).

• Heuristic Block Selection: They also tested a parameter-free selection heuristic inspired by Quest (select top-$n$ blocks by a simple score) (⇒) (⇒). This method avoids extra parameters by computing a block score (e.g. query • min-max of keys). They even tried a “cold start” training where the model was run with full attention for the first 1000 steps before switching to the heuristic sparse strategy (⇒), to help the model adjust. Despite this, the heuristic had low recall of truly important tokens (it often missed relevant blocks) and led to worse convergence (higher loss) than NSA’s method (⇒) (⇒).

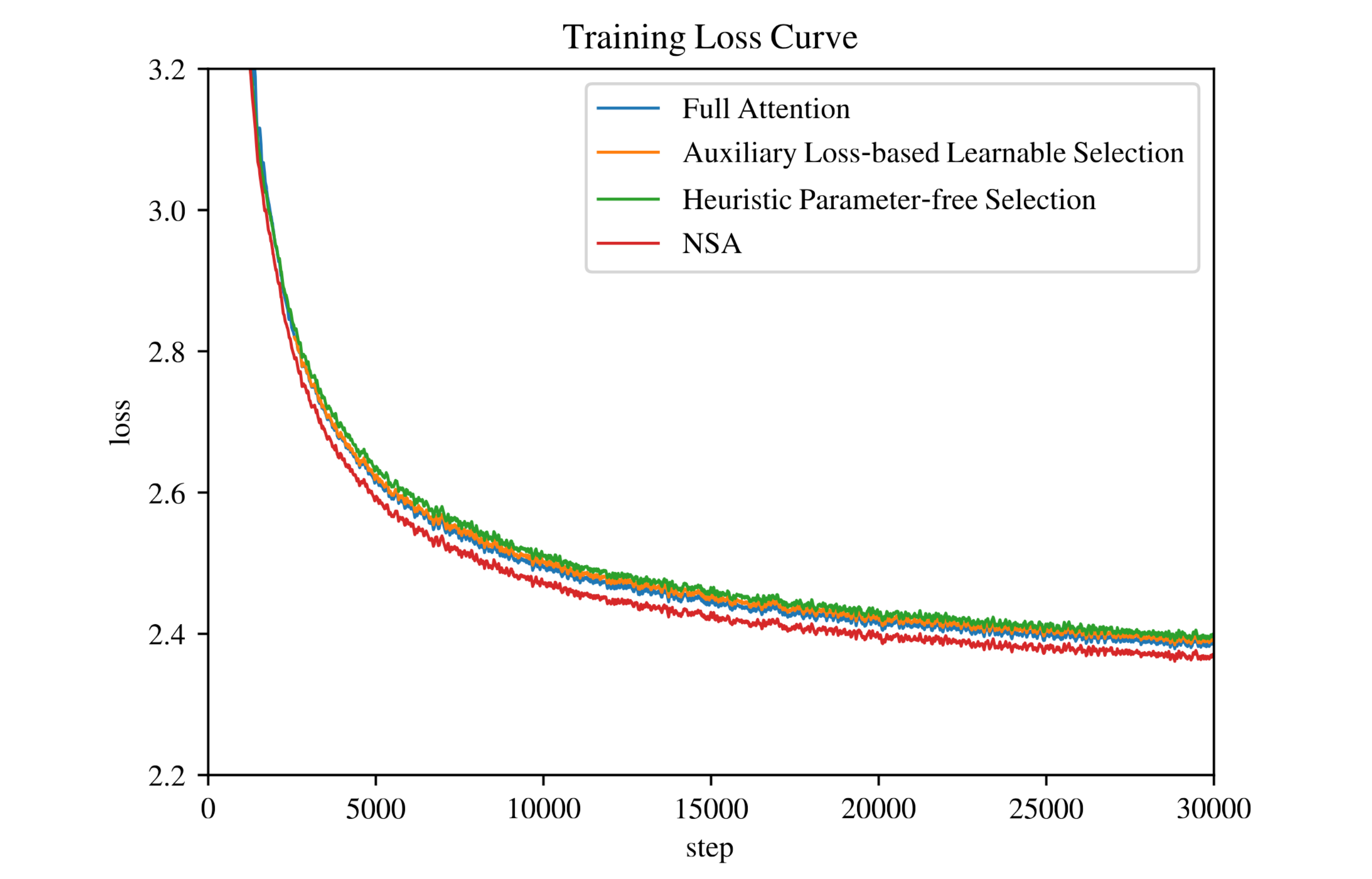
Figure 7 illustrates the training loss curves: both the auxiliary-learned selection and the Quest-style heuristic underperform Full Attention, whereas NSA achieves lower loss (better convergence) than either alternative (⇒) (⇒).

In summary, these ablations underscore why NSA was designed as it is. Approaches that explicitly select tokens or clusters during training proved either inefficient or harmful to quality. NSA instead opts for a hardware-aligned, hierarchical blocking strategy baked into the architecture, which avoids non-differentiable operations and heavy auxiliary costs. The ablation results show NSA’s approach yields better training performance than the tested alternatives, justifying the choices made in the NSA design.

5.2. Benchmarking NSA Performance

After training, NSA is benchmarked against the full-attention baseline (and other methods where applicable) to evaluate its accuracy, generalization, and task performance. The results show that NSA’s sparse attention does not sacrifice performance – and can even improve it – across a variety of tasks, despite using significantly fewer attention computations.

General Evaluation (Standard Benchmarks): On the suite of knowledge, reasoning, and coding benchmarks (MMLU, MMLU-PRO, CMMLU, BBH, GSM8K, MATH, DROP, MBPP, HumanEval), NSA matches or slightly exceeds the dense baseline’s accuracy on most tasks (⇒) (⇒). As summarized in Table 1, NSA outperforms the full-attention model on 7 out of 9 metrics, resulting in a higher average score (⇒) (⇒). For example, NSA shows notable gains on challenging reasoning datasets like DROP (+4.2% F1) and GSM8K (+3.4% accuracy) compared to the baseline (⇒). These improvements suggest that NSA’s training induced the model to focus on the most pertinent parts of the input, effectively filtering noise and honing in on key information, which can enhance performance on reasoning tasks (⇒). Even on knowledge-heavy tasks (MMLU and variants) and coding tasks, NSA’s performance is on par with or slightly above the dense model (⇒). This is remarkable given that NSA processes far fewer attention pairs — in other words, sparsity did not degrade quality. (Indeed, many evaluation samples in this setting are well within the local window size of NSA, so in those cases NSA behaves almost like full attention (⇒). The key result is that when sparsity does come into play, it doesn’t hurt accuracy.) The convergence of NSA’s performance with Full Attention across diverse short-context tasks demonstrates NSA’s robustness as a general-purpose architecture (⇒).

Long-Context Evaluation: In the extreme context length regime, NSA clearly shines. Figure 5 shows that in a 64k-length needle-in-a-haystack retrieval test (where a model must find a specific relevant snippet in a 64k token context), NSA achieves 100% retrieval accuracy across all positions (⇒) – effectively perfect performance – whereas dense attention would be infeasible to even run at this length without optimizations. NSA’s hierarchical attention design (coarse-grained compression + fine-grained selection) allows it to efficiently scan through long contexts and still attend to crucial details (⇒) (⇒). The coarse compressed tokens give it global awareness to identify which region of the context is relevant, then the fine selected tokens focus on the important details in that region (⇒). This two-level mechanism enables NSA to maintain high accuracy even as context length grows.

On the LongBench suite of tasks (with input lengths often beyond the full-attention window), NSA outperforms all the sparse baselines and even the full-attention model on most metrics (⇒) (⇒). Table 2 compares NSA, full attention, and other methods across various LongBench tasks. NSA achieves the highest average score overall (about 0.469 vs. 0.437 for full attention) (⇒) (⇒). In particular, NSA demonstrates strong gains on multi-document and long-range reasoning tasks: for instance, it beats the dense baseline by +8.7% on HPQ and +5.1% on 2Wiki multi-hop QA tasks (⇒). It also excels in long-context code understanding (LCC task, +6.9% over full attention) and passage retrieval (PassR-en, +7.5%) (⇒) (⇒). These substantial improvements underscore that NSA is not just matching full attention at long lengths, but actually leveraging its sparse architecture to handle long-context challenges more effectively (⇒). The authors note that NSA’s native sparse pretraining likely helped the model learn to “focus on task-optimal patterns” for long contexts (⇒), whereas methods that apply sparsity only at inference time can miss such optimization. Even on LongBench tasks where full attention was feasible, NSA often slightly outperforms it, indicating the sparse attention didn’t miss relevant information. (There are a few cases where NSA is marginally lower – e.g., one of the QA subtasks – but those are small trade-offs, and NSA still leads on average (⇒) (⇒).)

It’s worth noting that all other sparse methods (H2O, Quest, etc.) were configured to the same sparsity as NSA for fairness, yet NSA still did better on most long tasks (⇒). This suggests that NSA’s learned sparsity (through pretraining) is more effective than fixed or heuristic sparsity patterns. Additionally, because NSA can be used during training, it had the advantage of long-context fine-tuning, whereas the other methods could not be fine-tuned on those tasks (they lack training support) (⇒). This likely contributed to NSA’s superior long-context results and highlights a core advantage of native sparse attention.

Chain-of-Thought Reasoning: For complex reasoning, the NSA variant fine-tuned on long chain-of-thought data (NSA-R) demonstrates improved problem-solving ability compared to its full-attention counterpart. After supervised fine-tuning on 32k-token mathematical reasoning traces (distilled from a larger reasoning-specialized model), NSA-R achieves higher accuracy on the AIME 2024 challenge problems than the dense model under the same conditions (⇒). Table 3 reports the results: at an 8k token generation limit, NSA-R scores 0.121 vs. 0.046 for the full model, and at 16k tokens NSA-R scores 0.146 vs. 0.092 (⇒). In other words, NSA more than doubles the problem-solving success rate of the 27B model on these challenging math questions. This advantage persists even when allowing the models to use longer reasoning chains (16k tokens) (⇒). The authors conclude that NSA’s sparse attention patterns, learned during pretraining, help the model capture long-range logical dependencies needed for multi-step reasoning (⇒). Moreover, NSA’s hardware-aligned design retains enough contextual information (thanks to the combination of global and local attention paths) that the model can extend its reasoning depth without forgetting earlier parts of the chain (⇒). The fact that NSA-R outperforms Full Attention-R at both 8k and 16k context lengths validates that sparse attention, when properly integrated and trained, is viable for advanced reasoning tasks (⇒). In summary, NSA not only speeds up long-context processing, but can also improve a model’s ability to reason through lengthy, complex problems – a very promising result for the applicability of sparse attention in future AI systems.

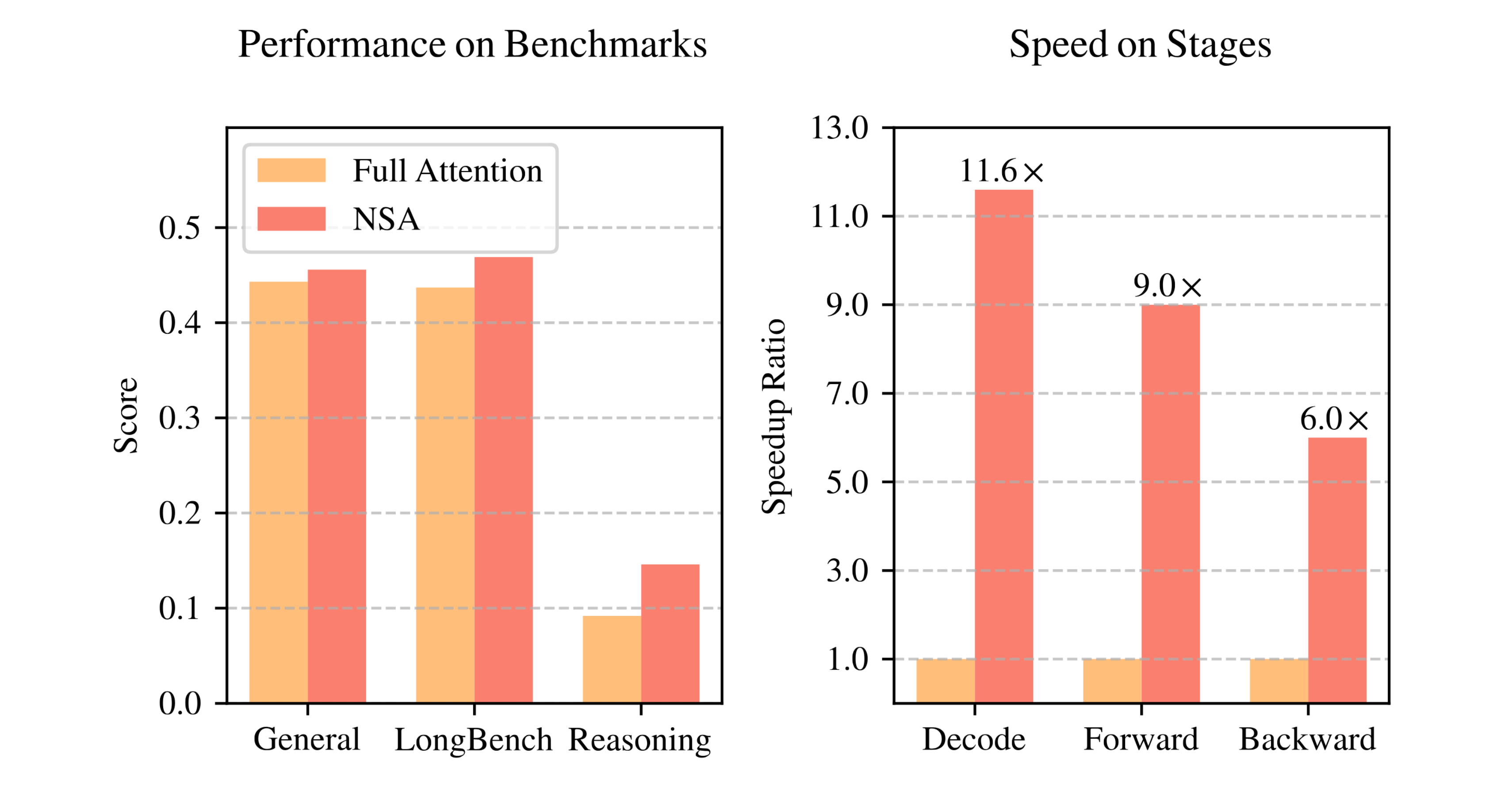
Figure 1 (left) provides a high-level summary, showing NSA slightly surpasses Full Attention on average performance across general, long, and reasoning benchmarks (⇒).

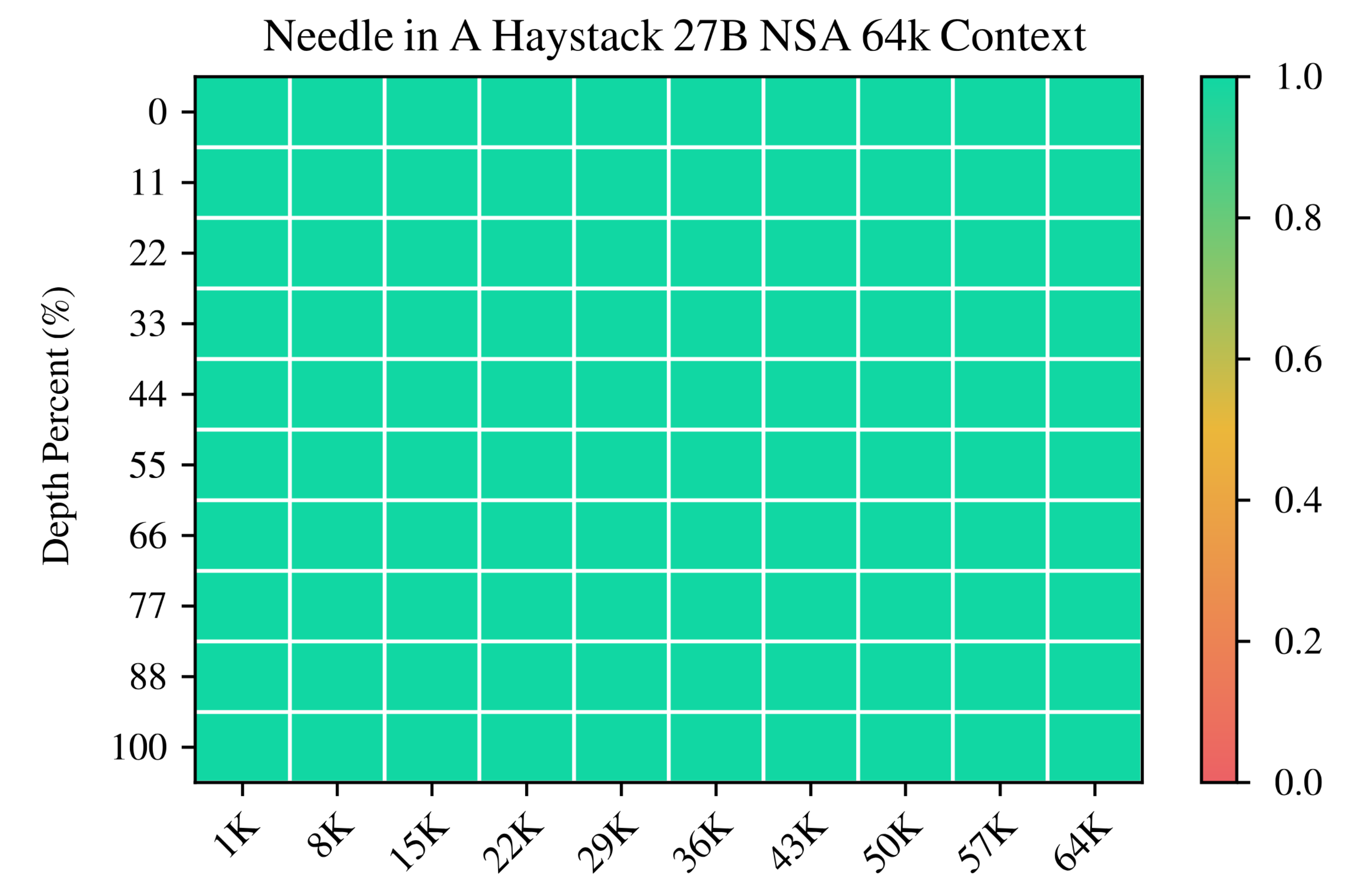
Meanwhile, Figure 5 illustrates NSA’s perfect accuracy in a 64k token retrieval task, highlighting its effective long-range attention capability (⇒).)*

5.3. Efficiency Analysis – Speedup and Scalability

A key motivation for NSA is to improve computational efficiency of attention for long sequences. The paper provides extensive measurements of training and inference speedups, showing that NSA achieves significant acceleration over standard full attention, especially as sequence length grows. The efficiency gains come from a combination of algorithmic sparsity (less work per query) and low-level optimization aligning with hardware characteristics.

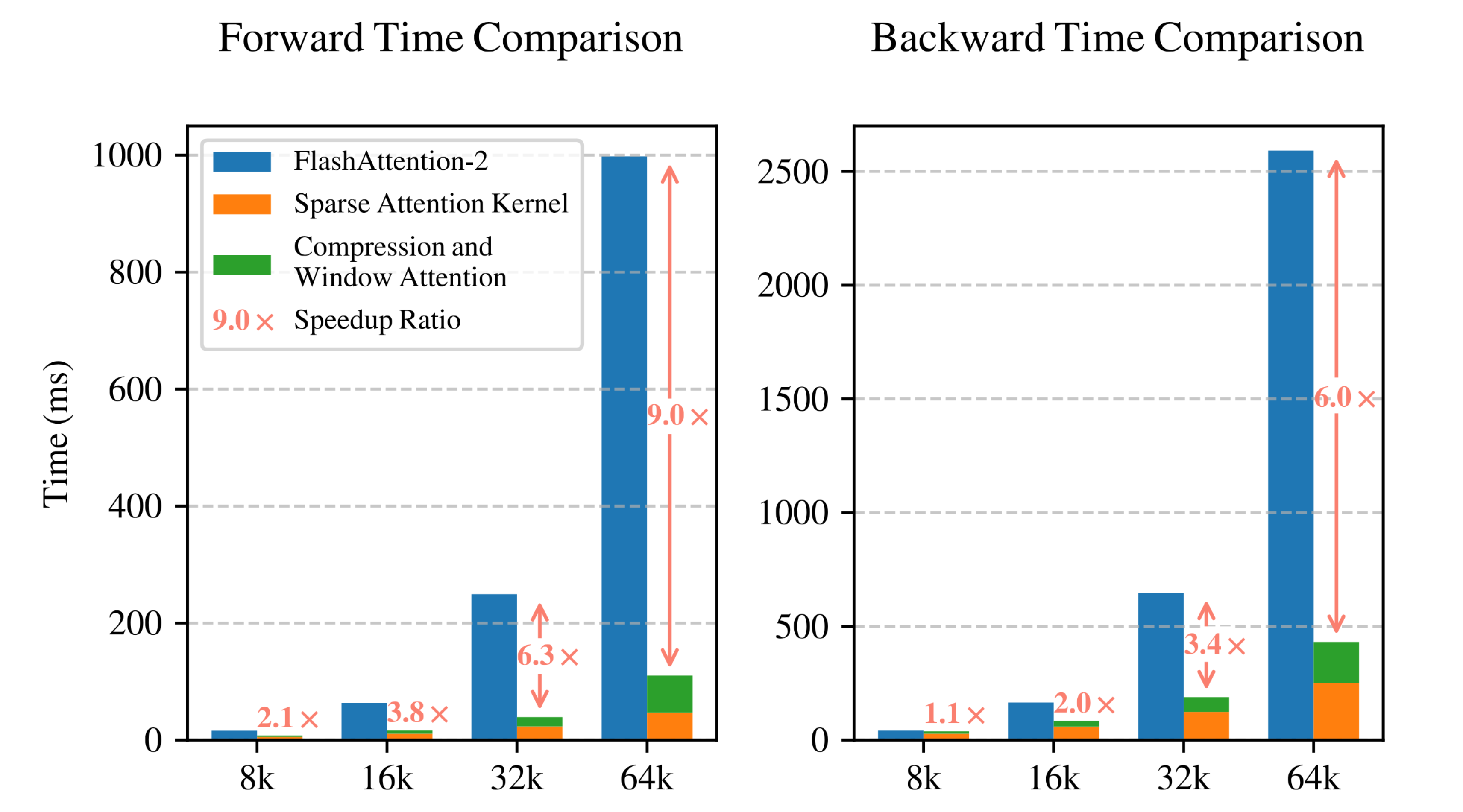
Training Speedups: The authors benchmarked the custom NSA attention kernel against the standard full-attention (dense) computation and against an optimized dense implementation (FlashAttention-2) on the same hardware (⇒) (⇒). All kernels were implemented in Triton for a fair comparison on an 8×A100 GPU setup (⇒) (⇒). Results (see Figure 6) show that NSA’s sparse attention yields increasing speed benefits at longer sequence lengths (⇒). For example, at a modest 8k sequence, NSA’s forward pass is about 2× faster than FlashAttention-2 (and >2× vs. naive full attention), while at 64k tokens it is about 9× faster (⇒) (⇒). Backward (training gradient) computation is similarly accelerated – roughly 6× faster than dense attention at 64k length (⇒) (⇒). The speedup scales nearly linearly with sequence length, becoming more pronounced with longer inputs (⇒) (⇒). This trend aligns with the algorithm’s complexity: full attention is $O(n^2)$ per forward/backward pass (or $O(n)$ per token for training), whereas NSA reduces the work per token dramatically for large $n$. Crucially, these training speedups are achieved without degrading convergence or final performance, as shown earlier. Thus, NSA manages to cut training time (especially for long-context training) significantly while preserving model quality.

Decoding/Inference Efficiency: In autoregressive decoding (generation), attention computation becomes a severe memory-bandwidth bottleneck for long contexts. NSA’s design drastically reduces the memory access needed at each generation step. In each decoding step, a full-attention model must read all $s$ past tokens’ key/value vectors from memory (where $s$ is the current sequence length). In NSA, by contrast, each query attends only to a sparse subset: at most $((s - l)/d)$ compressed tokens, $n l'$ selected tokens, and $w$ neighbor (local) tokens (⇒). Plugging in NSA’s typical settings (e.g. compression block size $l=32$, stride $d=16$, selected block count $n=16$ with block size $l'=64$, and local window $w=512$ (⇒) (⇒)), the memory load per step is thousands of tokens instead of tens of thousands. For instance, at $s=64\text{k}$, NSA would load roughly 5.6k token-worth of key/value data (compression + selected + local) instead of 64k, over a 11× reduction in memory traffic (⇒). Table 4 in the paper quantifies this, and indeed NSA achieves up to 11.6× lower latency than full attention at 64k context during decoding (⇒). The authors note that in this memory-bound regime, speedup is roughly linear with the reduction in memory access volume (⇒). Because NSA skips the majority of keys when context is long, its decoding throughput is far higher. In practical terms, this means generating text with a 64k context that might take a full-attention model, say, 1 second per token can be done by NSA in ~0.09 seconds per token (an order of magnitude speedup). The advantage grows with context length – at 32k, NSA was about 6× faster in decoding, and by 64k it’s >11× (⇒) (⇒).

Key Efficiency Techniques: NSA’s efficiency is not only from doing less work (sparse computation), but also from how that work is executed on hardware. The authors implemented a specialized attention kernel to maximize throughput on GPUs:

• Blockwise Coalesced Memory Access: NSA processes queries in blocks and fetches keys/values in contiguous chunks that align with GPU memory lanes. This coalesced, blockwise access pattern keeps the high-bandwidth memory (HBM) and on-chip SRAM busy with large, efficient transfers (⇒). By organizing computations on tiles of the attention matrix, NSA can utilize Tensor Cores effectively, achieving high FLOPs utilization even though the attention is sparse.

• Loop Scheduling to Eliminate Redundant Transfers: The kernel is carefully structured so that each key/value token in the sparse set is loaded from memory only once and reused for all necessary computations (⇒). NSA’s attention uses a grid-loop over query groups and an inner loop over fetched KV blocks (as illustrated in Figure 3), which ensures that data stays in fast on-chip memory (registers/shared memory) while a block of queries is processed (⇒). This avoids the inefficiency of naive sparse implementations that might reload the same key blocks for different heads or query segments. Overall, the custom kernel minimizes memory stalls and makes the sparse computation compute-bound instead of memory-bound.

Thanks to these optimizations, NSA converts theoretical complexity savings into real speedups. The Triton-based implementation effectively leverages GPU hardware features (memory hierarchy, parallel threads, tensor operations), yielding the near-linear scaling of speedup with sequence length observed in the experiments (⇒). The design also scales well with model size and multi-GPU setups. The authors trained and tested NSA on 8×A100 GPUs, and the attention kernel can be parallelized across GPUs similarly to standard attention (each GPU handling a portion of the batch or sequence) (⇒). Thus, NSA’s approach is scalable in both the batch/model dimension and in sequence length. It enables training giant models on long sequences within practical time: for example, without NSA, pretraining on 32k contexts might be prohibitively slow or memory-heavy, but NSA makes it tractable by both reducing per-step compute and memory load.

In summary, NSA achieves its efficiency gains through a combination of algorithmic sparsity (doing less work) and low-level optimization (doing the work efficiently). The result is substantial speedups in both training and inference for long-context scenarios, which scale up with longer sequences. This directly addresses the bottlenecks of vanilla attention, making NSA a highly practical solution for long-context deep learning.

Figure 6 (see above) illustrates the speedups: NSA’s custom kernel has significantly lower forward/backward runtime than FlashAttention, with speedup ratios growing from ~2× at 8k to 9× at 64k for forward pass (⇒).

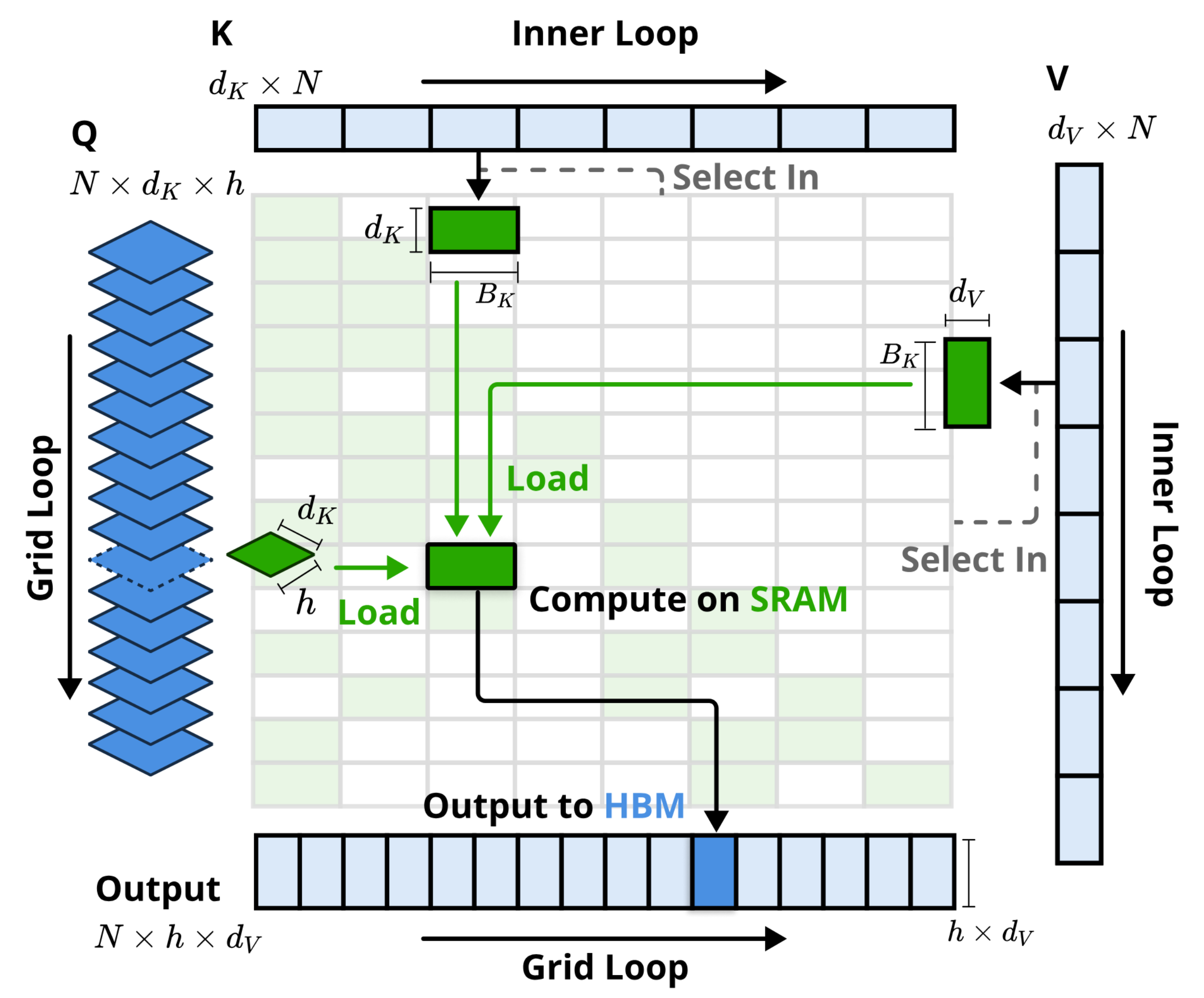
Figure 3 depicts the kernel’s blockwise execution strategy (grid loop over query groups and inner loop over KV blocks) that enables these optimizations (⇒).

5.4. Visualization, Limitations, and Future Directions

Attention Pattern Visualizations: To gain insight into why NSA’s block-based approach works, the authors analyzed the attention distributions of a fully trained model.

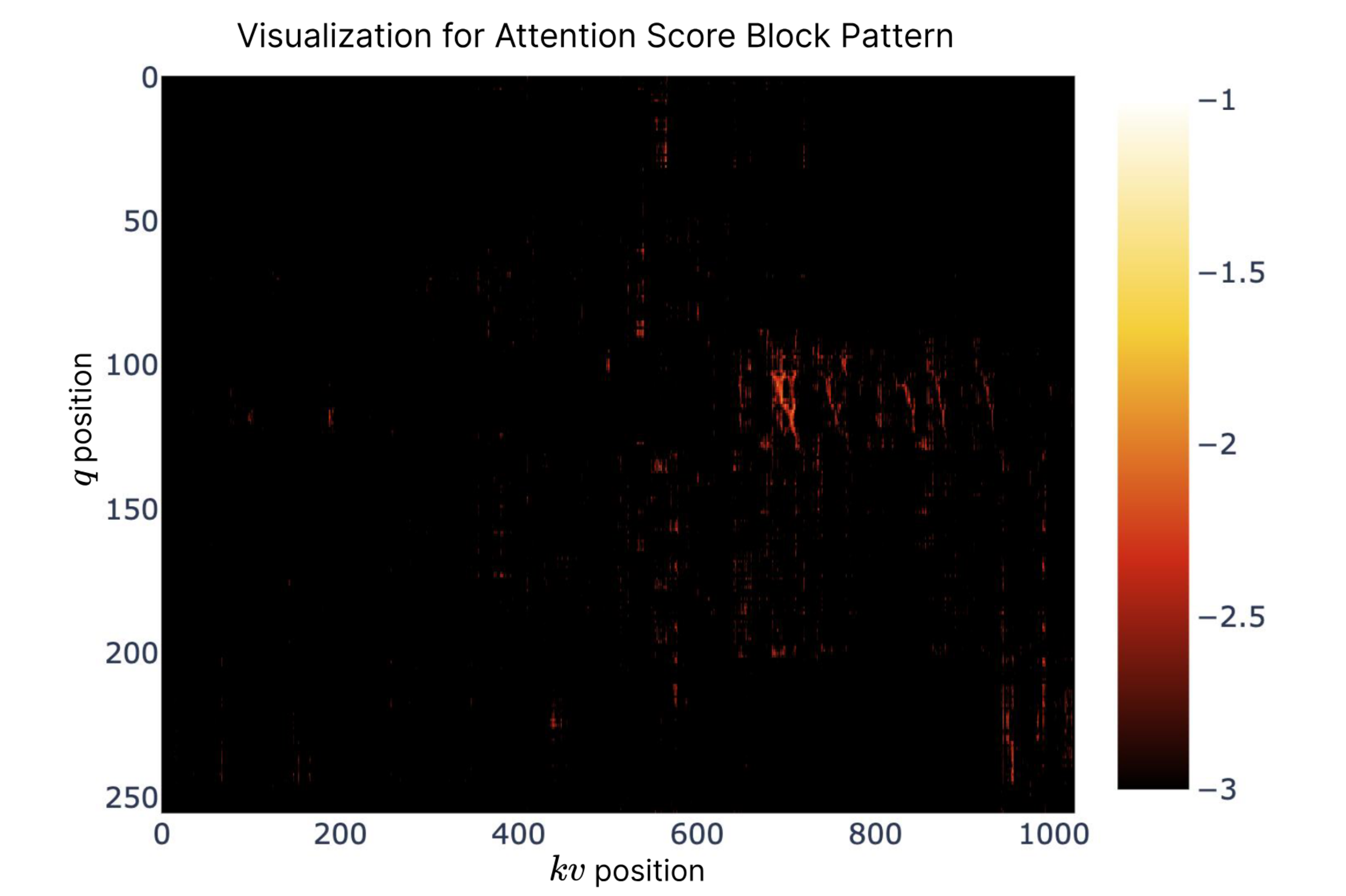
Figure 8 provides a visualization of the attention score matrix from a pretrained 27B full-attention Transformer (⇒).

Interestingly, the heatmap of attention shows a blockwise clustering pattern: queries tend to attend to contiguous runs of keys with similar intensities (⇒). In other words, if a token strongly attends to another token, it often also attends to its neighboring tokens with comparable strength, forming light-colored blocks on the map (⇒). This empirical observation supports NSA’s design principle that nearby tokens share semantic relevance for a given query (⇒). The NSA mechanism explicitly takes advantage of this by selecting whole blocks of tokens (after compression) rather than scattering attention to arbitrary individual tokens. The visualization lends credence to the idea that a continuous block of text can often be treated as a meaningful unit for attention – possibly because of topical coherence or the way information is distributed in text. The authors note that the exact nature of these relationships (why exactly adjacent tokens often carry similar attention weight) “requires further investigation” (⇒), but it clearly provided inspiration for NSA. Thus, Figure 8 effectively illustrates how NSA’s block selection is aligned with actual attention patterns observed in large LMs, explaining why NSA can drop many tokens yet still capture the important context.

The paper also visualizes the training dynamics for different sparse strategies (Figure 7, discussed earlier in Section 1) to highlight NSA’s advantage. In that plot, NSA’s training loss stays lower than the alternatives, whereas the heuristic and auxiliary-loss methods show higher loss (worse performance) throughout training (⇒) (⇒). This visualization emphasizes that naive implementations of sparse attention can lead to learning difficulties, whereas NSA’s method learns as smoothly as full attention. Together, Figures 7 and 8 help readers intuitively understand NSA’s benefits: Figure 7 shows NSA is easier to train, and Figure 8 shows NSA is focusing on the right structures in the data.

Limitations: While NSA demonstrates strong results, the authors acknowledge a few limitations and open challenges in their discussion. First, many existing sparse attention methods could not be directly trained end-to-end – NSA’s development revealed that incorporating sparsity into training is non-trivial, requiring careful design (as evidenced by the failures of the initial clustering or learned-selection attempts) (⇒) (⇒). This means that truly adaptive sparse attention (where the model dynamically decides which tokens to attend without any fixed pattern) remains challenging. NSA’s solution was to use a fixed hybrid scheme (compressed + local + selected blocks) that is trainable; however, this comes at the cost of having several hyperparameters (block size, number of blocks, etc.) and a predetermined structure. In scenarios where the optimal pattern of sparsity might change drastically, a more flexible approach could be beneficial. The authors note that methods relying on learned importance scores introduced overhead and sometimes degraded performance (⇒), so one limitation is that NSA does not incorporate a fully learnable token selection mechanism – it avoids that to remain efficient and effective. Future research may explore making the sparsity more content-adaptive without falling into the traps identified (excessive overhead or non-differentiability).

Another limitation is that NSA’s advantages really manifest at long sequence lengths; for shorter sequences (within a few thousand tokens), NSA behaves similarly to full attention (and indeed the efficiency gains are smaller) (⇒) (⇒). This isn’t so much a drawback as an expected trade-off – sparse attention isn’t needed when everything fits in cache – but it means that NSA’s complexity is only worth it if long contexts are actually used. For tasks always in the short range, full attention or simpler local attention might suffice. NSA also required a custom kernel implementation to achieve its potential. This indicates a practical limitation: implementing NSA on other hardware or frameworks would require similar low-level optimization work. Without tuning the algorithm to the hardware, the theoretical speedups might not materialize (as has been seen with some prior sparse methods that lacked kernel support) (⇒). However, since the authors have demonstrated it on GPUs with Triton, this provides a template for future implementations.

It’s important to note that the paper does not report any significant accuracy limitations of NSA on the tested benchmarks – in fact, it generally improved or matched performance. One could speculate that in tasks requiring extremely fine-grained attention to widely separated tokens (e.g. if truly random long-range dependencies occur that don’t exhibit block structure), NSA’s blockwise approach might miss something. But the benchmarks (even diverse ones like LongBench) did not expose any catastrophic failures; NSA’s results were uniformly strong. The authors do suggest that understanding why certain tokens end up attended together (the block pattern phenomenon) is an open question (⇒). So a limitation in the scientific sense is the lack of theoretical understanding of sparse attention patterns – it’s observed that it works, but we don’t fully know how optimal or universal the approach is. This paves the way for more analytical future work.

Future Directions: The authors explicitly state that analyzing attention patterns has provided “valuable context for future research directions.” (⇒) Based on the discussion, a few key avenues for future work emerge:

• Understanding and Modeling Attention Patterns: Further research could delve into why transformer attention naturally clusters in blocks and whether this holds across architectures and data. A deeper understanding could lead to new sparsity schemes that are even more effective or adaptive. For instance, if we can characterize when two tokens have redundant influence on a query, models could be taught to merge or compress such tokens on the fly. This line of inquiry bridges model interpretability and efficient architecture design.

• Differentiable Sparse Selection Mechanisms: Given the difficulties the authors faced with auxiliary losses and heuristics, an important future direction is finding ways to allow the model to learn which tokens to attend (and which to ignore) without incurring huge training overhead or instability. This might involve novel continuous relaxations of the selection process or new training objectives. Success here would combine the best of both worlds: the adaptability of learned sparsity with the stability and speed of NSA’s fixed scheme. It could broaden the applicability of sparse attention to scenarios where the optimal sparsity pattern is data-dependent.

• Longer Contexts and New Domains: NSA was tested up to 64k context in language tasks. Future work might push this boundary further (e.g. 100k+ tokens or even infinite context via streaming) and also apply NSA to other domains. Domains like vision or multimodal tasks could benefit from similar sparse attention to handle high-resolution inputs or long video frames. The impact of NSA-like approaches on those domains remains to be explored.

• Integration with Advanced Training Paradigms: The chain-of-thought experiment in the paper used knowledge distillation for reasoning. A future direction is applying NSA in full reinforcement learning from human feedback (RLHF) or other complex training loops for LLMs. The authors referenced a reinforcement learning approach (DeepSeek-R1) aimed at improving reasoning (⇒). While they avoided RL for the 27B model due to scale, as models get larger (and NSA helps keep training efficient), one could attempt RLHF or other policy optimization directly with a sparse-attention model. This could unlock even better reasoning and alignment capabilities in long-context models.

• Broader Impact on Efficiency: From a systems perspective, NSA opens the door to training and deploying economical long-context models. Future research might quantify the energy savings and cost reduction of using sparse attention at scale, and explore hybrid models where some layers use dense attention and others use NSA to balance speed and accuracy. The broader impact is making large models more sustainable and accessible by cutting down the computational load.

In essence, NSA’s findings encourage a re-examination of transformer architecture: do we really need all-pairs attention all the time? The success of NSA suggests many tokens can be skipped or compressed without loss, which is a insight future models will likely exploit. We may see new architectures that generalize NSA’s ideas (hierarchical attention, multi-resolution context) to achieve even greater efficiency. Sparse attention research will also look into formal guarantees – e.g., how to ensure no important token is dropped – and into learning sparse patterns dynamically. The authors’ work is a step toward trainable sparsity, and they hint that continuing in this direction (with the lessons learned) is a promising path for the field.

5.5. Conclusion

The evaluation of NSA (Native Sparse Attention) demonstrates that it is possible to achieve drastically improved efficiency in long-context processing without sacrificing – and sometimes even enhancing – model performance. Through comprehensive experiments, Part 5 of the paper showed that NSA matches or exceeds the accuracy of dense attention on a wide range of benchmarks, including knowledge tests, reasoning problems, and coding challenges (⇒) (⇒). NSA particularly excels in very long-context and reasoning-intensive tasks, validating the idea that a well-designed sparse attention mechanism can capture essential information even in sequences tens of thousands of tokens long. This is a significant result in the landscape of transformer research: it dispels the notion that we must choose between speed and accuracy. NSA delivers both, by focusing computation on the most relevant portions of the input.

From an efficiency standpoint, NSA sets a new state-of-the-art in long-context attention. Its hardware-aligned design yields order-of-magnitude speedups (up to 10× or more) in both training and generation when dealing with long sequences (⇒) (⇒). These practical gains mean that models can be trained on longer sequences using the same compute budget, or conversely, that given a fixed sequence length, NSA uses far less time and memory than standard attention. In real-world terms, NSA can enable large language models to actually utilize 32k–64k token contexts in production, where before it would have been too slow or costly. This has broad implications – for example, long documents or multi-document queries can be handled more readily, and tasks like lengthy dialogues or books summarization become more feasible. NSA effectively brings the theoretical benefits of sparse attention to fruition by bridging the gap between algorithm and hardware, something prior sparse methods struggled with (⇒).

Another key insight from the paper is that sparsity can augment capability: NSA’s model wasn’t just efficient, it sometimes outperformed the dense model (especially on multi-hop reasoning and retrieval tasks) (⇒). This suggests that removing extraneous attention connections might reduce distraction and help the model focus, much like an information bottleneck that improves generalization. It’s a profound observation that cutting out 90% of the attention computation can, if done correctly, yield a better model. In the broader sparse attention research, this will encourage approaches that treat sparsity as a feature, not just a necessary evil for speed.

In conclusion, NSA represents a significant advancement in sparse attention for transformers. It proves that native trainability – integrating the sparse mechanism from pretraining onwards – is crucial to reaping the full benefits of sparsity. The authors’ evaluation, discussion, and forward-looking remarks paint a picture where future large models might routinely use architectures like NSA to handle long contexts efficiently. The impact of NSA could be far-reaching: by dramatically lowering the computational barrier for long-context modeling, it enables AI systems that can read and reason over longer texts, logs, or transcripts than ever before. Overall, NSA demonstrates that with innovative architecture design and hardware-conscious optimization, we can push the limits of sequence length and model reasoning ability, ushering in a new generation of scalable, powerful transformers for tasks that were previously out of reach due to attention complexity.

(The analysis above is based on Part 5 of the paper and related discussions (⇒) (⇒). The figures and tables referenced (Figures 4–8 and Tables 1–4) correspond to the key experimental results and illustrations provided by the authors.)